Author | Xi Nanhua

Source | Mathematical Translation Forest

Quantity and shape are the basic attributes of matter and things. They are the objects of mathematical research, which determines the value and significance of mathematics.

Mathematics is actually concerned with the mathematical laws of quantity and shape, which is a reflection of the real world. The law of mathematics is the law of the basic attributes of matter and things, and it is the most essential part of the laws of nature and society.

The meaning and value of mathematics seems needless to say, but the language of mathematics is abstract, and the abstract face is basically that people don’t like it, and it is often mistaken for being far away from the real world and human fireworks, which is quite unjust. The abstract value will be mentioned later.

1. What was mathematics like in the distant past?

Mathematics has a long history. It is generally believed that mathematics, as an independent and theoretical discipline, appeared between 600 BC and 300 BC, and Euclid’s Elements (about 300 BC) is a brilliant model.

It systematically sorts out the mathematical achievements of ancient Greeks by using axiomatic system, and its system, the expression of mathematical theory and the way of thinking embodied in the book have far-reaching influence on the development of mathematics and even science. Throughout the history of mathematics development, The Original is the most influential mathematics book.

Another great mathematical work in ancient Greece was apollonius’s "Conic Curve", which was later than "The Original" in time. In addition to synthesizing the achievements of predecessors, this book has unique innovation, excellent material organization and flexible writing. This book can be called the pinnacle of conic curve, and later generations can hardly say anything new on this subject, at least geometrically.

Almost at the same time, there was a study of the history of mathematics. Eudemus (about 370-300 BC), a student of Aristotle (384-322 BC), wrote books on the history of mathematics.

The history of human civilization is much longer. About 10 thousand years ago, human beings began to settle in a region and live by agriculture and animal husbandry. Writing appeared much later, around 3200 BC. Before that, the progress of human beings in mathematics was extremely slow, because the level of development was low, the demand for mathematics was extremely low, and it was very difficult to form abstract mathematical concepts from scratch.

The most basic concepts of mathematics, numbers and straight lines, took a long time to form.

At first, people’s concept of logarithm was associated with specific objects, such as a tree, a stone, two people, two fish, and so on. Time, constantly passing, … Gradually, people realized the common numerical attribute of a tree, a stone and other concrete objects, and the abstract concept of number was formed.

Similarly, at first, people’s concept of line was associated with specific line shapes such as trees, branches, ropes and edges of objects. Time goes by … gradually, people realize the common shape attributes of concrete objects such as straight trees, taut ropes and straight edges of some objects, and the abstract concept of straight lines is formed.

The formation of the concepts of number and straight line is a leap for human beings to understand nature.

The emergence and development of mathematics is driven by real life. Arithmetic and geometry were first produced.

Realistic needs have led to the calculation between numbers (such as distributing food, exchanging goods, the number of days before the specified date, etc.). So you need to give the number a name and write it down and tell others.

Digital symbols introduced from the beginning of writing have played a great role in the development of arithmetic.

This is the first step to introduce general mathematical symbols and formulas. In the next step, the introduction of arithmetic operation symbols and unknown symbols was completed very late, and it was constantly improved. For example, the familiar symbols of addition, subtraction, multiplication and division were not used until the 15th and 18th centuries.

Arithmetic was first developed in Babylon and Egypt, due to the practical needs of taxation, land measurement, trade, architecture, astronomy and so on. But here is mainly for the calculation and answer of specific problems. This form of arithmetic is not a mathematical theory, because there is no general property (or law) about numbers.

The transition to theoretical arithmetic is gradual. Ancient China, Babylonia and Egypt already knew the possibility of millions. Here has shown the possibility of infinite continuation of the series. But people didn’t realize this clearly soon.

Archimedes (287-212 BC) pointed out the method of naming the number of a large number of sand grains in the Sand Counting Law. This is a matter that needs to be explained in detail at that time. It’s not an easy thing today.

In the third century BC, the Greeks clearly realized two important ideas: the sequence of numbers can continue indefinitely; We can not only use specific numbers, but also discuss general numbers, and establish and prove the general properties of numbers.

For example, there are infinitely many proofs of prime numbers in the elements, and this conclusion and proof will be mentioned later. Arithmetic thus developed into theoretical arithmetic.

Theoretical arithmetic is actually the theory of numbers, and the calculation of specific local problems is not its main content, but the establishment of the laws and general properties of numbers by concepts and reasoning is its main content. Of course, this will, in turn, be helpful to specific calculations at a higher level.

The convincing source of theoretical arithmetic: its conclusion is drawn from the concept by using logical methods, and both logical methods and arithmetic concepts are based on thousands of years of practice and the objective laws of the world.

The concepts and conclusions of theoretical arithmetic reflect the nature and relationship of the quantity of things, summarize a lot of practical experience, and show the relationships that are often encountered everywhere in the real world in an abstract form. The objects can be animals, agricultural products and planets.

Therefore, the abstraction of arithmetic is not empty, but through long-term practice, it summarizes some universal properties, which has wide application. The same is true for all mathematics and any abstract concepts and theories. The possibility of wide application of the theory depends on the extensiveness of the original materials summarized in it.

Abstraction has its own limitations: when applied to specific objects, it only reflects one aspect of the object, and often only quantity is not enough. You can’t apply abstract concepts everywhere indefinitely. A sheep and a wolf are added together, and a liter of water and a handful of soil are not the place where arithmetic plus one is applied. Truth is concrete and mathematics is abstract. The application of abstraction to concreteness is often an art and technology.

The development of numbers is also very interesting. At first, it is a number associated with a specific object, then an abstract number, and then a general number. Each stage relies on previous concepts and accumulated experience. This is also one of the basic laws of the formation of mathematical concepts.

The origin and development of geometry is similar to that of arithmetic. The actual needs of measuring and calculating the area of land and the volume of containers, the volume of barns and water conservancy projects have led to the emergence and development of geometry, including the concepts of length, area and volume. For farmers, knowing the area of land is very beneficial to predict the harvest. For water conservancy projects, it is important to know how long the earthwork volume will take to complete the project.

Babylonians and Egyptians were the leaders in the initial years of geometric development (about 3000 BC to 700 BC). At first, geometry is some formulas summed up from experience, including the formulas for finding the area of triangles, rectangles, trapezoid, circles, cuboids, spheres, etc.

The formula A=(8d/9)2 used by the Egyptians to calculate the area of a circle was surprisingly good at that time, where d was the diameter. This formula is equal to taking π=3.1605 from the area formula of a circle. Geometric problems are also arithmetic problems in calculation.

Babylonians and Egyptians should not have realized at that time that their algorithms and rules needed to be based on, or could deduce some conclusions from others through deduction. The formulas or laws they get are not related to each other, so they are not systematic.

At this time, the Greeks appeared. They went to Egypt and Babylon to do trade, travel and study math and science. In this way, the arithmetic and geometry of the Egyptians and Babylonians spread to Greece around the seventh century BC. Then came the era when the stars shone and there were many schools of thought. Interestingly, China was roughly in the Spring and Autumn Period and the Warring States Period, with a hundred schools of thought contending, and many thinkers came forth: Laozi, Confucius, Mozi, Mencius, Zhuangzi, Xunzi and Han Feizi.

The influential schools in the classical Greek period (from 600 BC to 300 BC) are: Ionian School, Pythagorean School, Ernian School, Clever School, Plato School, Aristotle School, etc.

The most important ideological contributions of the ancient Greeks to mathematics include: mathematics studies abstract concepts, and all mathematical results must be deduced by deduction according to the axioms clearly defined in advance.

Geometry thus develops in the direction of geometric theory; Introduce concepts, draw conclusions from experience, clarify the relationship between them, and find new conclusions. In this process, abstract thinking plays an extremely important role. In the spatial form of real objects, geometric concepts are abstractly generated: points (without size), lines (without width and thickness), surfaces (without thickness).

Like arithmetic, geometry comes from practice and gradually forms mathematical theory. Geometric theory studies the abstract forms and relationships of space.

This is different from other sciences that study the spatial form and relationship of objects, such as astronomy and measurement, or art such as painting and sculpture. It is impossible to do experiments in abstract space form, and only logical reasoning can be used to establish the connection between conclusions and derive new conclusions from known conclusions.

The obviousness of geometric concepts, the method of reasoning and the convincing conclusion are all based on thousands of years of practice and the objective laws of the world, just like arithmetic.

When we emphasize the importance of interdisciplinary to scientific development today, looking back at history, we will find that it is a specious formulation.

The intersection of disciplines has been very active in history, which is an important source of further general concepts, methods and theories, and has a great impact on the development of human civilization and science. The greatest scientists, such as Archimedes, Newton, Leibniz, Euler, Gauss and Einstein, have made great contributions in many aspects.

Let’s say that arithmetic and geometry, the earliest two branches of mathematics, were inseparable and influenced each other from the beginning. Simple length measurement is already a combination of arithmetic and geometry. When measuring the length of an object, put a single position of a certain length on the object, and then count how many times it is put together. The first step (placement) is geometric, the geometric concept behind it is congruence or coincidence, and the second step (number) is arithmetic.

When measuring, it is often found that the selected unit cannot be placed on the measured object for an integer number of times. At this time, the unit must be divided, so that a part of the unit can be used to measure the object more accurately, that is to say, not only the integer, but also the fraction can be used to represent the length of the measured object.

The score is thus generated. This is the result of the cooperation between geometry and arithmetic, which produces an important new concept-fraction, and causes the popularization of the concept of number from integer to fraction.

The discovery of irrational numbers also comes from the combination of geometry and arithmetic, but the discovery of irrational numbers cannot be realized by measurement, because the accuracy is always limited in actual measurement, and irrational numbers are infinite acyclic decimals.

Pythagorean theorem tells us that the diagonal length of a square with unit side length is the square root of 2, which is an irrational number. In this way, the concept of number is further developed. Moreover, people gradually understand the number as the ratio of a certain quantity to the quantity taken as a unit.

The discovery of irrational numbers is a typical example that reflects the power and profundity of mathematical theory in revealing natural laws and phenomena. Without mathematics, many phenomena and laws can’t be understood.

The further development of number is the concept of real number, and then the concept of complex number. Then there is the algebraic structure.

Hua Luogeng, the late great mathematician, made an incisive comment on the relationship between logarithm and form: when the number is missing, it is less intuitive, and when the number is missing, it is difficult to be nuanced.

—————————-

1. The original poem: number and shape are interdependent, so how can they be divided into two sides? When the number is missing, it is less intuitive, and when the number is missing, it is difficult to be nuanced; The combination of numbers and shapes is good, and everything is separated; Don’t forget, the unity of geometry and algebra is always connected and never separated! See Selected Poems of Hua Luogeng, China Literature and History Publishing House, 1986.

2. number (sh) number (sh)

Speaking of it, mathematics should start with numbers (sh) and numbers (sh). Who among us can’t count? Soon after we can talk, our parents will tell us to count, and our ability to count will definitely be greater when we get to kindergarten. We usually count

1, 2, 3, 4, 5, 6，……

It seems that most people don’t think of counting all the integers with positive integers. In fact, this is possible, and a number method is:

0, 1，-1, 2，-2, 3，-3，……

In this way, all the integers are counted with positive integers.

Ordinary people should not even think of counting rational numbers (fractions) with positive integers. Intuitively, this seems impossible. Surprisingly, this is also possible.

Fractions can be written as the ratio of integers: 0, p/q, where p and q are positive integers not equal to 0, and there is no common factor greater than one.

First, according to the size of the value of p+q, it is divided into several parts to sort, and each part is counted again, so one number method is:

0，1，－1，1/2，2，－1/2，－2，1/3，3，－1/3，－3，

1/4，2/3，3/2，4， －1/4，－2/3，－3/2，－4，……

In this way, we also counted the rational numbers with positive integers.

Curiosity certainly can’t end like this. We may wonder how to count real numbers with positive integers. This time there is really nothing to do: positive integers can’t count real numbers clearly. This can be strictly proved, but we won’t talk about it here, although it is not difficult.

The story is not over yet.

A question arises here: Is there a set of numbers between the whole of natural numbers and the whole of real numbers, which can’t be counted by positive integers (that is, it can’t establish a one-to-one correspondence with natural number set), and real numbers can’t be counted by this set?

Cantor, the founder of set theory (a branch of mathematics), suspects that such a set does not exist. This is the famous continuum hypothesis. Hilbert gave a report at the International Congress of Mathematicians in 1900, and listed 23 problems, the continuum hypothesis being the first one. This shows the importance of this issue. These 23 problems have a great influence on the development of mathematics in the future.

Godel is a great mathematical logician. In 1940, he proved that there is no contradiction between the continuum hypothesis and the axiomatic system we usually use. Just because there is no contradiction doesn’t mean it is right.

In 1963, Cohen established a powerful method-the forced method. By this method, he proved that there is no contradiction between the hypothesis of continuum and the axiomatic system we usually use. That is to say, in our commonly used axiom system, adding this assumption will not produce contradictions; If this assumption is not added, there will be no contradiction.

This is obviously beyond the expectation of ordinary people. An important and natural question cannot be judged true or false in our commonly used axiomatic system. This shows the strangeness of logic. Cohen won the Fields Prize in 1966 for his work on the continuum hypothesis.

The continuum hypothesis seems to have been understood, but in fact, the thinking on this issue has not stopped, and profound mathematics is still being produced.

We can compare the continuum hypothesis with the parallel axiom of plane geometry. The thinking and research on parallel axioms leads to the emergence of non-Euclidean geometry such as hyperbolic geometry. Riemannian geometry is a kind of non-Euclidean geometry and a mathematical framework of general relativity.

Curiosity, simple good questions can always take us far, far away.

3. Know infinity

In our limited life, it seems to be a difficult thing to know infinity, and it may even be a disturbing thing. The ancient poem "Born less than 100 years old, always worried about being a thousand years old" shows that we are not willing to be confined to our limited time and space.

But infinity is awesome. Pascal said, "When I think of my short stay in life, swallowed up by the eternity before and after, and the small space I occupy, submerged by the infinite and vast space that I know nothing about, I feel scared. The eternal silence of these boundless spaces scares me. "

There are infinite integers and infinite real numbers. In the game of counting, we know that these two infinity are essentially different.

Only mathematics can study the infinite, reveal the magical infinite world, and use the infinite to study the limited. Examples include limit, series, infinite set …

The following two equations can make people feel the infinite magic of mathematical utilization:

—————————-

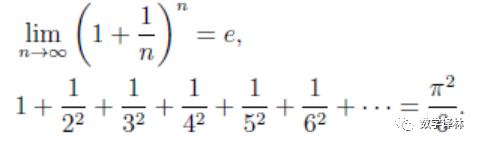
2.When I consider the short duration of my life, swallowed up in an eternity before and after, the little space I fill engulfed in the infinite immensity of spaces whereof I know nothing, and which know nothing of me, I am amazed. The eternal silence of the infinite spaces frights me. Blaise Pascal, in "pensé es" (originally in French, meaning meditation), 1670.

Hilbert, a great mathematician, has a profound understanding of infinity: "No other problem has ever touched people’s hearts so deeply;" No other thought can stimulate people’s logical understanding of thinking so fruitfully; However, there is no other concept that needs to be clarified more than the concept of infinity. "

4. Some opinions

Great people never skimp on their awe and praise of mathematics:

Mathematics is the core of reality.

-Pythagoras School, Plato School

We often hear the view that "everything is number" comes from Pythagoras, and he has a similar expression: number rules the universe; Number is the essence of everything. Plato School was deeply influenced by Pythagoras School and put mathematics in the highest position: the highest form of pure thought is mathematics.

On the gate of Plato’s Academy, it is written that "those who have no knowledge of geometry are not allowed to enter this gate".

In the seventh chapter of Plato’s Republic, there is a long dialogue to discuss the importance of arithmetic and geometry. The conclusion is that arithmetic forces the soul to use pure reason to lead to truth, geometry is to know eternal things, and arithmetic and geometry are the first and second courses that young people must learn.

Mathematics is the true essence of nature.

-ancient Greece

With this understanding, it seems not surprising that ancient Greece can make epoch-making achievements in mathematics.

Physics is written in the big book of the universe, and it keeps opening before our eyes. But we can’t read this book until we learn to write the characters and language of the universe. It is written in mathematical language, and the characters are triangles, circles and other geometric figures. Failure to understand these means that it is impossible for human beings to understand every word of this book. Without these, people can only wander in the dark maze.

-Galileo

—————————-

3.“Das Unendliche hat wie keine andere Frage von jeher so tief das Gemüt der Menschen bewegt; das Unendliche hat wie kaum eine andere Idee auf den Verstand so anregend und fruchtbar gewirkt; das Unendliche ist aber auch wie kein anderer Begriff so der Adfkl?rung bedürftig.” David Hilbert: In address (4 Jun 1925), at a congress of the Westphalian Mathematical Society in Munster, in honor of Karl Weierstrass. First published in Mathematische Annalen (1926), 95, 161-190 with title über das Unendliche.

Galileo was one of the founders of modern experimental science and mechanical materialism. He established the law of falling body, discovered the law of inertia, and determined the "Galileo relativity principle". He is a pioneer of classical mechanics and experimental physics. He was also the first person who made great achievements in observing celestial bodies through telescopes. Galileo’s view of mathematics can be regarded as a development of the view of the ancient Greeks.

Mathematics is the queen of science.

-Gauss

Gauss is known as the prince of mathematics in the 19th century, the greatest mathematician in the 19th century, and an outstanding physicist, astronomer and geodetic scientist. His words are often quoted, but I don’t know where Gauss took the emperor.

In natural science, mathematics is incredibly effective.

-eugene wigner

Wigner put forward the theory that the nucleus absorbs neutrons and discovered the Wigner effect, so he won the Nobel Prize in Physics in 1963.

This introduction was the topic of Wigner’s report in Courand Institute of Mathematics of new york University on May 11th, 1959. The article was published in the journal Communications in Pure and Applied Mathematics sponsored by Courand Institute of Mathematics in February, 1960. This view of Wigner has a great influence, and the discussion and extension of this view have never stopped since it came out.

—————————-

4.Philosophy (i.e. physics) is written in this grand book, the universe, which stands continually open to our gaze. But the book cannot be understood unless one first learns to comprehend the language and read the letters i n which it is composed. It is written in the language of mathematics, and its characters are triangles, circles, and other geometric figures without which it is humanly impossible to understand a single word of it; without these, one wanders about in a dark labyrinth.” Galileo Galilei, The Assayer (Il Saggiatore (in Italian)), as translated by Stillman Drake (1957), Discoveries and Opinions of Galileo pp. 237-8.

5. "Die Mathematicist Die Knigin der Wissenschaft en und Die Zahlen Theorist Die Knigin der Mathematik", Wolfgang Sartorius von Waltershausen: Gauss Zum Ged Chtnis (Biography of Gauss), 1856.p.79. 。

God is a mathematician of very high rank. He used very advanced mathematics when he built the universe. Our attempt to be weak in mathematics enables us to understand a little bit of the universe. As we continue to develop more and more advanced mathematics, we can hope that we can better understand Universe 6.

-Dirac

Dirac discovered a fruitful new form of atomic theory, so he won the Nobel Prize in Physics with Schrodinger in 1933. The Dirac equation he put forward was hailed as a groundbreaking work, which predicted the existence of positrons and was later confirmed by experiments. The δ function he proposed was very creative and shocking, which was unacceptable in the mathematical theory at that time, but it was very useful in physics.

Later, when the generalized function theory appeared, mathematical theory could explain and deal with the δ function, which turned out to be a generalized function.

Mathematics must control our rational flight; Mathematics is a crutch for the blind. Without it, it is difficult to move. Everything in physics is undoubtedly due to mathematics and experience.

-Voltaire

Voltaire was a French philosopher and writer in the 18th century and a leading figure in the French bourgeois enlightenment. His thoughts represented the thoughts of the whole Enlightenment, enlightened people’s minds and influenced a whole generation.

The strength of French mathematics is not only the achievement of French mathematicians, but also profound cultural factors.

The development and perfection of mathematics is closely related to the prosperity of the country.

-Napoleon

Napoleon was a great French strategist and politician in the 19th century, and the founder of the First Empire of France. People generally pay attention to his military and political achievements. In fact, his achievements in science and education are also crucial to the future development of France.

During the First Empire of France, France established a national education system that has been preserved to this day, and established public middle schools and French universities to train talents and encourage the rise of scientific research and technical education.

—————————-

6. “God is a mathematician of a very high order, and He used very advanced mathematics in constructing the universe. Our feeble attempts at mathematics enable us to understand a bit of the universe, and as we proceed to develop higher and higher mathematics we can hope to understand the universe better.” P. A. M. Dirac: The Evolution of the Physic ist’s Picture of Nature. Scientific American, May 1963, Volume 208, Issue 5.

7. “Mathematics must subdue the flights of our reason; they are the staff of the blind; no one can take a step without them; and to them and experience is due all that is certain in physics.” Francois Marie Arouet Voltaire, Oeuvres Completes, 1880, t. 35, p. 219.

8. “The advancement and perfection of mathematics are intimately connected with the prosperity of the State.” Napoléon Bonaparte: Correspondance de Napoléon, t. 24 (1868), p.112．

Napoleon paid great attention to science and culture. After taking power, he regularly attended the meetings of the French Academy of Sciences, invited academicians to report on scientific progress, and awarded many awards to scientists, including foreign scientists.

Napoleon’s concern promoted the prosperity of French science, and a large number of dazzling scientific stars appeared, such as Laplace, Lagrange, Gaspard Monge, sadi carnot, Fourier, Gay-Lussac, Lamarck and Ju Weiye.

Mathematical science presents one of the most brilliant examples. Without the help of experience, pure reason can successfully expand its territory.

-Kant

Kant was a German philosopher in the 18th century and was considered as one of the greatest philosophers of all times. He has profound knowledge of natural science and a deep understanding of morality. His philosophy has a profound influence on German classical philosophy and western philosophy, and also on the birth of Marxist philosophy. Critique of Pure Reason is his most famous work.

Strange as it may sound, the strength of mathematics lies in its avoidance of all unnecessary thinking and its pleasant saving of mental labor.

-Mach

Mach was an Austrian physicist and philosopher from the 19th century to the early 20th century. The Mach number of high-speed flight is named after him. His most important achievement was that he found the shock wave when he was studying the high-speed motion of an object in gas. Mach’s Mechanics had a profound influence on Einstein. Mach has also been nominated by many people as a candidate for the Nobel Prize in Physics.

Mach’s above viewpoint is a specious truth, which will be explained later by the problem of the seven bridges in Konigsberg and the classification of crystals.

—————————-

9. “The science of mathematics presents the most brilliant example of how pure reason may successfully enlarge its domain without the aid of experience Immanuel Kant and F. Max Mü ller (trans.),’ Method of Transcendentalism’, Critique of Pure Reason (1881), vol. 2, p.610. See also: Critique of Pure Reason, p.575, by Kant, translated by Wang Jiuxing, Commercial Press.

10. “Strange as it may sound, the power of mathematics rests on its evasion of all unnecessary thought and on its wonderful saving of mental operations.” Ernst Mach: in E.T. Bell, Men of Mathematics (1937), Vol. 1, l (Roman numeral ‘l’)).

If I feel sad, I will do math and become happy; If I am happy, I will do math to keep happy.

-Renee

Alfréd Rényi is an outstanding Hungarian mathematician in the 20th century. He mainly studies probability theory, combinatorial mathematics, graph theory and sequence. Renee told us how good it is to do math!

Pure mathematical structure enables us to discover concepts and laws that relate to these concepts, and these concepts and laws give us the key to understanding natural phenomena.

-Einstein

One reason why mathematics enjoys special respect over all other sciences is that his propositions are absolutely reliable and indisputable, while all other scientific propositions are debatable to some extent and are often in danger of being overturned by newly discovered facts. There is another reason why mathematics has a high reputation, that is, mathematics gives precision nature a certain degree of reliability. Without mathematics, these sciences cannot achieve this reliability.

-Einstein

Einstein is the greatest scientist in the 20th century, and is well known to all women and children. Its scientific achievements have changed people’s understanding of the world.

He is not only a great scientist, but also a great philosopher and social activist, deeply concerned about the fate of mankind. The profound understanding of nature, society and human beings makes people marvel at his superhuman intelligence and great heart.

—————————-

11. “If I feel unhappy, I do mathematics to become happy. If I am happy, I do mathematics to keep happy.” Alfréd Rényi: In P. Turán, ‘The Work of Alfréd Rényi’, Matematikai Lapok (1970), 21, pp.199-210.

12. “pure mathematical construction enables us to discover the concepts and the laws connecting them, which gives us the key to understanding nature.” Albert Einstein, In Herbert Spencer Lecture at Oxford (10 Jun 1933), ‘On the Methods of Theoretical Physics’. Printed in Discovery (Jul 1933), 14, 227. Also reprinted in Philosophy of Science, Vol. 1, No. 2, (Apr., 1934), pp. 163-169. For Chinese translation, please refer to the first volume of Einstein’s Collected Works, translated by Xu Liangying and others, Commercial Press, 2010.p.448. 。

13.“One reason why mathematics enjoys special esteem, above all other sciences, is that its propositions are absolutely certain and indisputable, while those of all other sciences are to some

extent debatable and in constant danger of being overthrown by newly discovered facts. … But there is another reason for the high repute of mathemati cs, in that it is mathematics which affords the exact natural sciences a certain measure of certainty, to which without mathematics they could not attain.” Albert Einstein: Geometry and Experience, Published 1921 by Julius Springer (Berlin), also reprinted in “The Collected Papers of Albert Einstein”, Translation Volume 7, Princeton University Press, 2002. For Chinese translation, please refer to the first volume of Einstein’s Collected Works, translated by Xu Liangying et al., Commercial Press, 2010.p.217. 。

The universe is big, the particles are tiny, the speed of rockets, the cleverness of chemical engineering, the change of the earth, the mystery of biology and the complexity of daily use, and mathematics is everywhere.

-Hua Luogeng

Hua Luogeng’s comments on the use of mathematics are extremely incisive.

5. the spirit of exploring the world

In practice, knowledge is gained through sensibility and thinking. Furthermore, through abstract thinking, the connection between knowledge is established and science is formed. At this point, reason and thinking have their own free kingdom.

In one’s own kingdom, thinking often goes far beyond actual needs. For example, some large numbers such as one billion or ten billion are generated on the basis of calculation, and the actual needs of using them are later; Imaginary numbers are generated by solving the equation x2+1=0, and then they are widely used.

Mathematics is concerned with the mathematical laws of quantity and shape, and it is an elf to explore the world. In the free kingdom of thinking, it is dexterous and has a lot of free space to fly, and many achievements will take a long time to be applied after completion. Famous examples include:

The study of conic curve by Greeks more than two thousand years ago was used to describe the motion of celestial bodies in the 17th century.

L Riemannian geometry is the mathematical framework of general relativity.

The role of fiber bundle theory in gauge field theory.

The role of l matrix and infinite dimensional space in quantum mechanics.

The application of probability theory in statistical mechanics, biology and finance.

l ……

Our country’s culture and tradition are pragmatic, focusing on immediate interests. Here, I would like to quote the philosopher Whitehead’s advice:

"For those who limit their knowledge and research to obvious usefulness, there will be no more impressive warning, such as the following example: conic curves have been studied as abstract science for 1,800 years, without any practical consideration except to satisfy mathematicians’ thirst for knowledge. However, at the end of this long abstract research, they were found to be essential keys to acquire knowledge of one of the most important laws of nature."

—————————-

14. Hua Luogeng: "Great use of mathematics", originally published in People’s Daily on May 28, 1959. Reprinted in "Great Mathematics for Use" (selected works of Hua Luogeng’s popular science works), Shanghai Education Press.

6. The wisdom of mathematics

Most people are willing to stay away from mathematics, but Mach said that mathematics can save brains pleasantly (see the previous section 4: Some opinions), which is really confusing. Maybe Mach is talking about the wisdom of mathematics. We use two examples to illustrate this point.

The first example is the problem of the Seven Bridges in Konigsberg. This problem occurred in the 18th century, when Konigsberg was the city of Prussia, and now it is Kaliningrad, Russia. There is a river crossing the city, which divides the city into four parts, and there are seven bridges connecting these four parts, as shown in Figure 16 below.

It is said that a popular pastime of the citizens at that time on weekends was whether a route could be designed to cross each bridge just once. No one has ever succeeded, but that doesn’t mean it is impossible. In 1735, the mayor of Danz Creek (about 140 axioms west of Konigsberg) was entrusted by a local mathematician to find Euler. Euler was the greatest mathematician in the 18th century. At the age of 28, he was already famous.

—————————-

15. “No more impressive warning can be given to those who would confine knowledge and research to what is apparently useful, than the reflection that conic sections were studied for eighteen hundred years merely as an abstract science, without a thought of any utility other than to satisfy the craving for knowledge on the part of mathematicians, and that then at the end of this long period of abstract study, they were found to be the necessary key with which to attain the knowledge of one of the most important laws of nature.” A. N. Whitehead, Introduction to Mathematics, London WILLIAMS & NORGATE, pp110-111.

16. Source: https://plus.maths.org/content/bridges-k-nigsberg

Euler thought about the problem like this. The river divides the city into four parts, and the size of each part is not important. What matters is the route design of crossing the bridge. Thus, the land can be abstracted into points, and the bridge can be abstracted into connecting lines 17 between points.

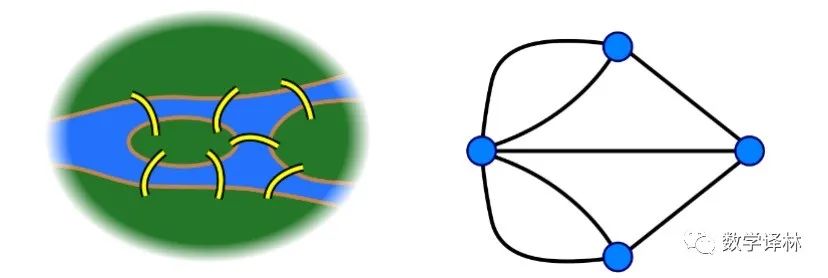
So the problem becomes to design a route on the right picture above, which passes through each connecting line (bridge) exactly once.

Suppose there is such a route. If a point is neither the starting point nor the end point, then the route to this point (that is, the bridge) is different from the route to leave this point. This requires that the number of lines connecting this point must be even.

The picture above has four points, and the starting point and ending point of a line add up to at most two. That is to say, no matter how the route is designed, at least two of the four points are neither the starting point nor the end point, and the number of routes connecting such points must be even. However, the lines (bridges) connecting the four points in the above picture are all odd numbers, namely, 5, 3, 3, 3. This means that it is impossible to design a route for the above picture, passing through each connecting line (bridge) exactly once.

Euler’s way of solving this problem shows the abstract value and the wisdom of mathematical thinking. Euler’s work also marked the birth of a branch of mathematics-graph theory. Graph theory is very useful in information science, including network and chip design.

The second example is the classification of crystals. Diamonds and snowflakes are crystals, which are very beautiful. Crystals have good symmetry. In fact, the symmetry of crystals has a strong constraint on the types of crystals. The branch of mathematics that studies symmetry is group theory. So mathematics has played a great role in the study of crystals. In 1830, German hessel (1796-1872) determined that there were 32 symmetrical forms of crystal shape (called 32 point groups).

—————————-

17. Two sources: https://plus.maths.org/content/bridges-k-nigsberg

After determining the symmetrical form of the shape, people turn to the internal structure of the crystal. Frangen Heim (1801-1869), a 19th century German, proposed that the internal structure of crystals should take points as the unit, and these points are arranged periodically in three-dimensional space.

Later, the French Blavy (A. Bravais, 1811-1863) put forward the theory of spatial lattice, which holds that the center of mass of the material particles in the crystal is distributed at the vertex, face or body center of the parallelepiped unit of the spatial lattice, and the particles are periodically arranged repeatedly in the three-dimensional space. They identified 14 forms of space lattice.

Abandoning all the physical properties of crystals and considering crystals only from the perspective of geometric symmetry, Russian crystallographer Fedorov determined that there were 230 kinds of microscopic symmetry forms of crystals, that is, there were only 230 kinds of spatial (symmetry) groups inside crystals.

Fedorov’s work was the mathematical theoretical basis of the later crystal experiment, which played a great role in determining the internal structure of the crystal. All these 230 symmetries were found in the experiment. In 1912, M．V．Laue, a German, revealed the periodic structure inside the crystal for the first time through X-rays, and confirmed the geometric theory of crystal structure.

Since then, the British father and son Prague (William Henry Bragg, 1862-1942; William Lawrence Bragg, 1890-1971) and Russian Ulf (георгий (юрий) викт). In particular, they measured some crystal symmetries that Fedorov thought were imaginary (that is, symmetries that existed only in theory).

Laue and Prague won the Nobel Prize in Physics in 1914 and 1915 respectively. In the future, there are many works about crystal research that won the Nobel Prize.

7. The beauty of mathematics

Mathematicians, as well as some physicists, have a strong feeling for the beauty of mathematics, and their pursuit for it is endless:

My job always tries to unify truth and beauty, but if I can only choose one or the other, I often choose beauty 18.

-Waier

Weil is probably the greatest mathematician after Poincare and Hilbert in the 20th century, and he also put forward the gauge field theory in physics. His book Group Theory and Quantum Mechanics was first published in 1928.

It is said that theoretical physicists at that time would put this book on the shelf, but they didn’t read it because the mathematics in it was too difficult. Wail seems to believe that beauty is a higher level of truth, because what we see and understand should be only a part of truth.

And beauty can often bring us to a more comprehensive truth.

Beauty is the first test: ugly mathematics has no place in this world.

-hardy

Hardy was an outstanding analyst in the 20th century and the most outstanding mathematician in Britain in his time. His Monologue of a Mathematician expresses his views on mathematics and has a wide influence.

God created the world with beautiful mathematics. When trying to express the basic laws of nature by mathematics, researchers should mainly strive for the beauty of mathematics.

-Dirac

—————————-

18. “My work has always tried to unite the true with the beautiful and when I had to choose one or the other, I usually chose the beautiful.” Hermann Weyl, In Obituary by Freeman J. Dyson, ‘Prof. Hermann Weyl, For. Mem. R.S.’, Nature (10 Mar 1956), 177, p. 458. Dyson notes that this was told to him personally, by Weyl who was “half joking”.

19.Beauty is the first test: there is no permanent place in the world for ugly mathematics. — G. H. Hardy: In it A Mathematician’s Apology (1940) . First Electronic Edition, Version 1.0, March 2005, Published by the University of Alberta Mathematical Sciences Society, Available on the worldwide web at http://www.math.ualberta.ca/mss/. has a Chinese translation: A Mathematician’s Pleadings.

20. “God used beautiful mathematics in creating the world.” “The research worker, in his efforts to express the fundamental laws of Nature in mathematical form, should strive mainly for mathematical beauty.” Paul A. M. Dirac: in Paul Adrien Maurice Dirac: Reminiscences about a Great Physicist (1990), Preface, xv; p.110.

Dirac’s feeling of mathematical beauty is unique. Dirac’s equation is the perfect combination of experiment and mathematical beauty. In Dirac’s view, the equation derived from the experimental results only at that time does not have mathematical beauty, so he modified the equation according to his own understanding of mathematical beauty, and predicted the existence of positrons according to the modified equation, which was later confirmed by experiments. Dirac’s view seems to have something in common with Weil’s.

Dirac should like his equation very much. He first met Feynman at a meeting. After a long silence, Dirac said to Feynman, "I have an equation. Do you have one?". I guess Feynman was very depressed at that time.

Mathematics, if viewed correctly, not only possesses truth, but also possesses supreme beauty.

-Bertrand Russell

Russell, a mathematician and philosopher, won the Nobel Prize in Literature. The History of Western Philosophy, written by him, looks at the history of western philosophy from the perspective of a philosopher rather than a philosopher historian. It has a unique perspective, clear context, smooth writing and no lack of humor. His understanding of beauty naturally has a very broad background.

………

There is no doubt that the meaning of mathematical beauty has some similarities with other beauties such as art in formal beauty, but it is more a beauty of thinking and logic, wisdom and has its own characteristics. Everyone’s understanding of the beauty of mathematics is different, but the following views are helpful to grasp some meanings of the beauty of mathematics:

W form: clear, concise, simple, original, novel, beautiful, the connection between different objects.

W connotation: profound, important, basic and rich in meaning.

W proof: clear, neat and ingenious

Let’s illustrate the above point with some examples.

The first example is Pythagorean theorem, which is called Pythagorean theorem in the west. Hooking three strands, four strings and five is a special case of this theorem, which was put forward by Shang Gao in the early Western Zhou Dynasty. This theorem says that the sum of the squares of two right-angled sides of a right-angled triangle is equal to the square of the hypotenuse:

—————————-

21. “Mathematics, rightly viewed, possesses not only truth, but supreme beauty.” Bertrand Russell, Essay, `The Study of Mathematics’ (1902), collected in Philosophical Essays (1910), pp.73-74.

The proof is simple. The area of the big square in the above figure is the square c2 of the hypotenuse, which is equal to the sum of the areas of the four right triangles inside and the area of the small square:

Simplify, expand and gain.

So a2+b2=c2.

The form and proof of this theorem can reflect the meaning of the form and proof part of the mathematical beauty mentioned above. This theorem is basic, and its connotation is profound and rich.

An application of Pythagorean Theorem: On the plane coordinate, the coordinate (x,y) of a point satisfies the equation.

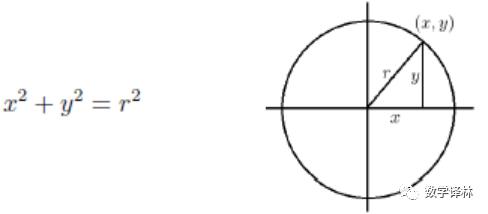
If and only if this point is on the circumference with radius r and the center of the circle is on the origin.

Pythagorean theorem is widely used, which is a manifestation of its basicity. Its profound connotation also lies in that many problems can be derived from it, such as:

What positive integers A, B and C can be the sides of a right triangle?

Is the area of a right triangle with integer sides an integer?

If the sides of a right triangle are all rational numbers, when is the area an integer (for example, 3/2, 20/3 and 41/6 are the three sides of a right triangle, and the area is 5. ) Such integers are called harmonious numbers or congruences.

The third question is closely related to the BSD conjecture of the Millennium problem. Who can solve the BSD conjecture, in addition to honor, can get one million dollars. 157 is a harmonious number, and the length of the three sides of the "simplest" rational right triangle with 157 as the area is:

The complexity and difficulty of the third question and BSD conjecture can be seen from this.

When talking about the meaning of beauty in mathematics, one of them is "the connection between different objects". This seems to have nothing to do with beauty, but it is actually a very important point of thinking, logic and wisdom. We look at Pythagorean theorem from this point of view.

Generally, people look at Pythagorean theorem as follows: knowing the length of two sides of a right triangle, we can find the length of the third side. This pragmatic thinking hinders our exploration and innovation. Looking at it from another angle, Pythagorean theorem reveals the relationship between the three sides of a right triangle.

This angle gives us a broad view at once. For example, the square of three numbers can be related to Pythagorean theorem or higher power:

This is the famous Fermat equation in number theory. Whether they have integer solutions without zero (that is, A, B and C are integers, but none of them are zero) is a problem that has puzzled mathematicians for more than 300 years.

In order to solve this problem, a great mathematics, algebraic number theory, has emerged, and now it is a very active research direction, with many famous scholars. The Fermat equation problem was finally solved by Wells in the 1990s, which was a great mathematical achievement in the last century. It was a sensation and the story behind it was unusually wonderful.

The second example is from Euclid’s Elements, which asserts that there are infinitely many prime numbers. There is a beautiful proof in Euclid’s book: If the conclusion is incorrect, then there are only a limited number of prime numbers, which are set as p1, p2, …, pn. Multiply them all and add 1 to get a number.

m＝1＋ p1p2 …pn

Then p1, p2, …, pn are not factors of M, so the prime factors of M are different from those N prime numbers. This is a contradiction, so there are infinitely many prime numbers.

This proof is neat and ingenious, which can make people feel happy mentally. Prime numbers seem easy to understand, but they are probably the most mysterious and elusive objects in mathematics. For prime numbers, it is easy to ask some questions that primary school students can understand, but the most intelligent mathematicians for hundreds of years can’t solve them.

For example, how much prime number occupies in natural numbers?

Goldbach conjecture: Every even number greater than 2 is the sum of two prime numbers.

Twin prime conjecture: There are infinitely many prime numbers P, so that p+2 is also a prime number.

The formulation of the first question is not clear enough. We can make the question more clear: how many prime numbers are there between 1 and n for any natural number n. Nobody can answer this question. But mathematicians have made a lot of progress.

At the beginning of 19th century, German mathematician Gauss and French mathematician Legendre put forward a famous conjecture about the proportion of prime numbers in natural numbers. At the end of 19th century, Adama and Dellavalle-Posen first proved this conjecture respectively, which is the famous prime number theorem. In 1949, Selberg and Erdis respectively gave elementary proofs of the prime number theorem. This is part of Selberg’s important work of winning the Fields Prize in 1950.

The second question is easy to understand, and it is easy to give examples, such as

12=5+7, 88=5+83=17+71=29+59=41+47， ….

So far, the best work on Goldbach’s conjecture is still the result of Chen Jingrun. His paper published in 1973 proved that every sufficiently large even number can be written as a prime number plus another number, and the number of prime factors of the other number does not exceed 2 (for example, prime numbers and 6=2×3 are such numbers, but 12=2×2×3 has three prime factors, which is not satisfactory).

Chen Jingrun’s result is known as Chen’s theorem in the world. In China, it has a misleading name: Chen Jingrun proved that 1+2 is a by-product of Xu Chi’s influential reportage "Goldbach conjecture".

Xu Chi’s reportage inspired a generation’s enthusiasm for mathematics and respect for Goldbach’s conjecture. Chen Jingrun also received a huge amount of letters of admiration and affection. This grand occasion never happened to mathematicians again.

Someone once told me about Chen Jingrun’s work, and he understood 1+2 completely literally. I tried to explain to him the meaning of 1+2 in Chen Jingrun’s work. He gave me an oblique look and said, "You don’t understand". I cried speechless and sighed deeply that it was not easy to do popular science.

At the same time, it is also found that sometimes people are obsessed with their own unrealistic understanding, which seems to be inseparable from their self-esteem and mental security.

The third question is also easy to understand. For example, 3, 5 and 41, 43 are all prime pairs with a difference of 2. The question is whether there are infinite such prime pairs.

In 2013, Zhang Yitang, a Chinese mathematician, made a great breakthrough in this issue. He proved that there are infinite pairs of prime numbers, and the difference between each pair of prime numbers is less than 70 million. Zhang Yitang’s result was a sensation, and the story that he kept pursuing his ideal in adversity was also very inspiring and touched the world.

Prime numbers are one of the most basic objects in mathematical research. So far, it seems that human beings have not shown enough intelligence to fully understand them. The most famous problem in mathematics is Riemann hypothesis, which is closely related to the study of prime numbers. In fact, Riemann put forward this conjecture at that time in order to study prime numbers. It is not surprising that Riemann’s hypothesis has not been solved yet.

The third example is the irrationality of the root number 2, which was a number that brought many troubles in ancient Greece. Theorem: If x2 = 2, then x is not a rational number.

We can also give an aesthetic proof. If the conclusion is incorrect, there will be integers a and b so that x = a/b. It can be assumed that a and b are coprime. Square both sides of XB = A, and you get X2B2 = A2. That is 2b2 = a2, so a is even and a = 2p.

So 2b2＝4p2 and b2 = 2p2, so b is an even number. Therefore, A and B are even numbers, and there is a common factor of 2, which is contradictory. So x is not a rational number.

Here, maybe we will suddenly think of whether pi, which was learned in primary school, is irrational? It seems that no one in primary school or middle school has talked about it. In fact, this is a good question, which is closely related to the famous problem of turning a circle into a square in ancient Greece.

This question says whether a square can be made only by ruler (without scale) and compass, and its area is the area of a given circle. It was not until Lin Deman proved the transcendence of π in 1882 that the answer was no.

Lin Deman’s work tells us that π is actually an extremely unreasonable number, called transcendental number, which is much more unreasonable than root number 2. The study of transcendental numbers is also very interesting and an important part of number theory. In the last century, Becker won the Fields Prize in 1970 for his research on transcendental numbers.

It is impossible to fully understand the beauty of mathematics without talking about its formal beauty. There are many important geometric objects in geometry that are extremely beautiful and amazing.

(1) Minimal surface: Minimal surface is very important in differential geometry. Minimal surface is the main tool in Qiu Chengtong’s proof of positive mass conjecture in general relativity.

(2) Fractal geometry: Fractal was discovered in the study of coastline in the last century, and later became an important branch of mathematics.

(3) Power system: Power systems are everywhere. The study of dynamic system in mathematics originated from Poincare’s study of three-body motion in astronomy, and now it is a very active branch of mathematics, and many people have won Fields Prize for the study of dynamic system.

—————————-

22. The following four color maps and the graphics in the next section are all from the Internet.

(4) Karabi-Chueh Manifold: Karabi-Chueh Manifold is a very important manifold, which has many researchers and plays a basic role in string theory.

There is no doubt that we can show the beauty of quality and form in mathematics indefinitely, but due to the limitation of space, we should give up this idea and leave more mathematical beauty to readers to explore.

8. Mathematicians

Mathematicians are a group of people with special talents, and their personalities and anecdotes are also colorful.

Weiner, the founder of cybernetics, is moving. On the day of moving, his wife repeatedly told him to go to the new address after work. Of course, as usual, Weiner forgot to return to the old site after work and found something different. I found a girl next to me in the dim light and asked, "I’m sorry, maybe you know me." I’m Norbert Weiner. We just moved. Do you know where we moved? " The girl replied, "Yes, Dad, Mom knew you would forget."

Wiener visited China in 1930s and gave lectures in Tsinghua. He appreciated Hua Luogeng very much.

Deligne was brilliant and won the Fields Prize for proving Wei Yi’s conjecture. He said: Whether you can do math problems is just a psychological problem. This is quite a bit like saying that I can do it, and saying that I can’t do it. This statement also echoes a widely circulated story.

One day, a student was late for a class in a cow university, and the class was over when he got to the classroom. There are seven topics left on the blackboard, which he thinks are homework. He will do these homework when he goes back. A week later, it was time to hand in homework. The student felt very painful. He only worked out two questions. Although he had a good idea for the third question, he had no time to finish it. When he threw his partially finished homework on the professor’s desk in frustration,

Professor: What is it?

Student: Homework.

Professor: What homework?

Only then did the students understand that what the professor wrote on the blackboard last week was the seven most important unsolved problems in this direction. It is said that this student has never done such an excellent job since he became a professional mathematician.

Hungarian mathematician Erdis is legendary, has no fixed residence, always travels, and cooperates with mathematicians there whenever he arrives, so the number of his collaborators is amazing. He believes that mathematicians are devices that turn coffee into theorems.

Siegel, a German mathematician, won the first Wolff Prize. He is a very smart and hardworking mathematician. Hiroyuki, a Japanese mathematician, won the Fields Prize. He often said that he was not talented, but he was meticulous and devoted himself to his work. When he first learned Algebra written by Vander Waals, he almost didn’t understand it, so he began to copy books until he understood it.

A mathematician talked about his late colleague: "He made many mistakes, but they were all made in a good direction. I tried to do this, but I found it difficult to make good mistakes. "

Physicist Kelvin (after whom Kelvin temperature is named) looks at mathematicians like this: Mathematicians are people who think the following formula is obvious:

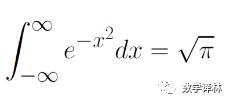
Descartes was a mathematician and philosopher. Mathematically, he founded analytic geometry. Philosophically, he put forward "I think, therefore I am", which caused people to think deeply about the relationship between consciousness and existence.

There is a rumor that he is in love with Princess Christina of Sweden, and the writing communication is blocked by the royal family, so he uses the equation r=a(1-sinθ) to express his passion. The princess quickly understood this unique love letter after reading it. This equation is a polar coordinate equation, and its image is

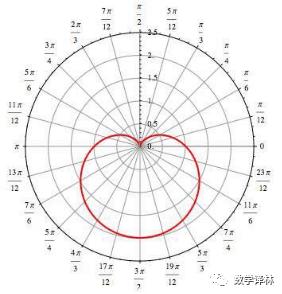
It seems that mathematics is not only a language to describe nature, but also a language to describe love.

This paper is based on the author’s report of the same name. Most of the materials in this paper are well known. The main reference materials for the historical part are as follows:

1. Mathematics, its contents, methods and significance, Volume I, A.D. Alexandrov et al., Science Press, 2001.

2. Ancient and modern mathematical thoughts, Volume I, by M. Klein, Shanghai Science and Technology Press, 1979.

Other references are quite complicated, including network resources, some of which are listed in the notes in the article, and there are still many references that are difficult to list one by one.

Welcome attention

Popularization of science Liaoning

Original title: "Academician Xi Nanhua: The Meaning of Mathematics"

Read the original text

On April 19th, Winter Olympics English volunteers came to Yaojiafang Primary School in Zhangjiakou.

Volunteers after 90s became attached to Winter Olympics.

Come to Zhangjiakou alone and pull up the volunteer team.

"Heads knees shoulders…… …" Accompanied by a simple and lively melody, pupils sang and danced under the guidance of volunteer teachers, with simple English words catchy and humorous and exaggerated movements full of movement. After singing a song, the children swarmed around Mr. Hou, scrambling to find him to sign his book and hand.

On the afternoon of April 19th, Hou Qunfeng, a post-90s volunteer, was treated like a star in the English class of Yaojiafang Primary School in Zhangjiakou.

Hou Qunfeng is the head of the Winter Olympics English Project of Zhangjiakou Charity Volunteer Association. He is 27 years old and is from Chenzhou, Hunan. Hou Qunfeng was born in a peasant family. He experienced the hardships of life from an early age and learned to give back to the society early. Since high school, he has been collecting waste products to support students with difficulties; In 2011, he was admitted to the English Department of Hunan University of Humanities and Science, and participated in voluntary service activities during his college years, serving as the head of a public welfare organization; Teach in a school for the deaf, and support more than 20 children by collecting waste.

In July 2014, Hou Qunfeng started his "one-dollar travel around the world" and joined the earthquake volunteer rescue twice during his journey.

In August 2014, Yunnan Ludian earthquake, he set up a rescue team and joined local militia to rescue three survivors. "I searched and rescued in the ruins once, but I didn’t have time to run, and I was buried alive once." He saved people and was saved by others.

In April 2015, Hou Qunfeng heard of a major earthquake in Nepal during his trip and decided to participate in the rescue. The rescue lasted for two months. He helped carry and distribute relief supplies, disinfected and prevented epidemic in disaster areas, and then began to raise funds to build schools, help school teachers take care of orphans together, and help organizations for the elderly, the sick and the disabled raise money …

In Nepal, Hou Qunfeng met Jia Qinghe, a volunteer from Zhangjiakou. In April 2017, Zhangjiakou Charity Volunteers Federation was established, with Jia Qinghe as the president. After receiving the invitation, Hou Qunfeng quit his job in Beijing and came to Zhangjiakou.

How to pull up the volunteer team when you are a stranger? In Hou Qunfeng’s own words, he was enthusiastic and "cheeky". A few days after he first came to Zhangjiakou, a foreigner in the street asked him for directions. "He is an international student of Hebei North College. I have been chatting and talking to him about the idea of forming a team of English volunteers for the Winter Olympics. He is also very interested and promised to try to mobilize his classmates. " As a result, Richy from Ghana became the first teammate. With their efforts, more than 400 students from Northern College joined the volunteer team. More and more volunteer groups in Zhangjiakou have also joined the Winter Olympics English Volunteer Service Team of the Charity Volunteer Association. In a year, the team has been expanding, with more than 2,000 registered volunteers, including foreign volunteers from more than ten countries, including Ghana, Bangladesh, Britain, Pakistan and Nepal.

The team is up, which groups are served? From the uncles and aunts in the community, to taxi drivers, hotel service personnel, to primary schools in urban and suburban areas, Hou Qunfeng began to "lobby". How can old people in their sixties and seventies persuade them? Hou Qunfeng figured out how to mark the pronunciation with Chinese characters, which made it easy for the elderly to remember. He took this booklet and walked around the streets, chatting with uncles and aunts to mobilize. How to arrange the time for primary school students to attend classes, and what content is suitable for teaching to lay the foundation for the next school textbook teaching? He contacted and communicated with the urban areas and surrounding schools one by one, and arranged students’ courses without affecting their daily courses.

Winter Olympics English class, the most passionate teacher

On the afternoon of 19th, three foreign students from North College attended Yaojiafang Primary School with Hou Qunfeng.

FJ has rich teaching experience. In class, FJ is persuasive, introducing English pronunciations of various parts of the body to children through cards and slides, and leading them to read aloud over and over again. Then divide the class into three groups, choose representatives to PK, listen to the words and point out the corresponding body parts, and the winner will get a "medal".

Hou Qunfeng, the founder of the volunteer service team, is with the children.

Vicky is a girl with a bright smile and affinity, and she is very popular among students. Every class, she will bring a lot of candy, and students who answer questions will get this sweet encouragement. Almost all students raise their hands to answer every question.

Among the three classes, the class led by John reads aloud the loudest. John’s reading is very vivid and his body language is varied. When he heard who had nonstandard pronunciation, he patiently corrected them one by one. Some students pronounced hair as head, and John grabbed his hair and reminded him over and over again until the pronunciation was correct, and high-fived them. "I can see you? John is actually a shy boy. " Hou Qunfeng said that John is a little shy on weekdays, and when he comes to class, he feels like a different person, and he is full of passion.

"Volunteer English class is the children’s favorite. It starts at 4 pm, and they are waiting in the classroom early." The teacher of Yaojiafang Primary School said. Gao Ruixue, a child from Class Two, Grade Two, told the reporter that he especially likes these volunteer teachers and is very fun and happy to learn English.

"We had classes on the fourth floor last year, and now we have changed to the first floor." Hou Qunfeng said with a smile that the classroom atmosphere was particularly High. He sang and danced with English songs and felt the floor shaking.

After the course, the students reluctantly bid farewell to the volunteer teacher. Some children quietly left a small gift for the teacher, a card made by themselves or a small doll on the podium.

"Although I am very tired, every time I see the children’s smiles, I feel that my work is valuable." Hou Qunfeng revealed that the current Winter Olympics English project covers more than 40 communities and nearly 40 classes in 10 primary schools in Zhangjiakou. His office is full of volunteer service schedules, and now there are more than 80 activities every week.

This team of English volunteers for the Winter Olympics is still expanding. "Our goal this year is to break through 3,000 people," Hou Qunfeng told reporters. In order to further popularize Winter Olympics English, they opened two English columns with Zhangjiakou TV and Zhangjiakou Daily. At the same time, we will jointly establish a volunteer team for consultation and translation with major hospitals in Zhangjiakou to provide translation volunteer services for foreign friends. Another preparatory team is a volunteer service lecturer group for sign language promotion jointly organized by Zhangjiakou Special School to prepare for the upcoming Paralympic Games.

Save the hero and form a team

We hope to have our rescue team in the Winter Olympics.

The Winter Olympics English Volunteer Service Team is one of the teams of Zhangjiakou Charity Volunteer Federation. At present, the Federation has a total of 95 volunteer teams with more than 8,000 registered members, and more than 30,000 volunteers are contributing to creating a civilized city for Zhangjiakou and welcoming the Winter Olympics.

As a winter Olympic city, it is an inevitable requirement to realize green travel. Zhangjiakou charity volunteer Green Zhangyuan Environmental Protection Team promotes environmental protection and advocates green travel, making green transportation a new business card for Zhangjiakou’s traffic development.

More and more Zhangjiakou people regard ice and snow sports as a new way of life, and major snow resorts have also attracted ice and snow sports enthusiasts from all over the country. The Winter Olympics is approaching, and a group of volunteers with professional rescue experience in Zhangjiakou are preparing for the ice and snow rescue team.

Shen Zhanjun, 50, is now the captain of the Emergency Rescue Corps of the Charity Volunteer Association. He was awarded the title of being a hero in Hebei Province and a model in Zhangjiakou. In 2017, the Qingshuihe Rescue Team was established.

Qingshui River is a tributary of Yanghe River in Yongding River system, which runs through Zhangjiakou city. "Every year in the summer, someone will fall into the river, sometimes more than 20 people a year. Last year, I discussed with a few like-minded friends and decided to set up a professional rescue team. " Shen Zhanjun introduced that there are currently 106 rescuers in the rescue team, with a total of more than 380 volunteers. More than 20 members come from Zhangjiakou Swimming Team and Zhangjiakou Winter Swimming Team, 4 of them hold national outdoor water rescue certificates and have rich experience in river rescue. In addition, there are more than 100 specialized drivers, medical care and logistics support personnel. According to the individual time, the team members will conduct uninterrupted inspections in three shifts from 5 am to 10 pm. "Last year we rescued 11 people and saved three people." Shen Zhanjun told reporters that in addition to water rescue, they also organized volunteers to set up an outdoor mountain rescue team and prepared to set up an ice and snow rescue team. At the end of last year, he proposed a plan to the Chongli District Government, and under the organization of the district government, he discussed with the heads of major ski resorts. "All major ski resorts have their own rescue teams, but after all, the scale is limited. If we gather together and set up an ice and snow rescue team through targeted training, it is much better than fighting alone and can improve rescue efficiency. " Shen Zhanjun is brewing this professional ice and snow rescue team that unites all forces. According to the plan, the selected players will receive a three-month professional training. "I hope that in the 2022 Winter Olympics, there will be an ice and snow rescue team set up by our Zhangjiakou volunteers themselves!" Shen Zhanjun said.

Source: Beijing Evening News reporter Zhao Xiao Road Intern reporter Li Huaren and photo

　　With solid and heavy production, "The Wind Rises in the Forest of Langya List" (hereinafter referred to as "The Wind Rises in the Forest") returned to the prime file of Beijing Satellite TV from the Zhoubo Theater. At present, the story is just halfway through, and the audience suddenly finds that the hero and heroine who really carry this costume drama are two young people — — When the play was filmed, Haoran Liu was only 19 years old and Zhang Huiwen was only 23 years old.

　　It is worth mentioning that it is no accident that Haoran Liu and Zhang Huiwen were both filming TV series for the first time, and they were selected by the team of nirvana in fire, which is famous for being critical and strict. Throughout the past two years, the role of Haoran Liu’s "circle powder" is not limited to Xiao Ping Jing, from Qin Feng, an alternative boy in detective chinatown, to Bailong, an infatuated teenager in The Legend of the Demon Cat, and even Lu Guichen in Kyushu, which is being filmed.

　　Lose weight desperately to get close to the role

　　Many people will refer to Haoran Liu’s strong "sense of youth" when evaluating him, but he himself knows that this is not the only thing to stand on. In order to be closer to the role image of The Wind Rises in the Forest, Haoran Liu tried to lose weight, and once his mouth was numb after dieting.

　　Not only did he study hard on the appearance of the characters, but he also studied the characters deeply. Before shooting, he spent a long time deconstructing the characters. Haoran Liu was only 19 years old when filming The Wind Rises in the Evergreen Forest. He was also worried that the audience would think that Xiao Ping Jing’s transformation from a teenager to a young Xia was "pretending to be mature". "So I set Xiao Ping Jing as a teenager full of dreams. With the development of things, this teenager slowly saw the world clearly, and he knew the world and also knew it.

　　The precise interpretation made director Kong Sheng also praise Haoran Liu’s performance as amazing, but he himself said modestly: "I feel that every role I play is very serious. I have not failed every role, and every role has not failed me."

　　I’ll crush Xiao Ping Jing for you.

　　As a huge fan of nirvana in fire, Haoran Liu thinks that the biggest difference between the two plays lies in their narrative methods. Different from the narrative way of mending and restoring the truth in nirvana in fire, The Wind Rises in the Forest is even more cruel. "It is to crush a beautiful thing to you."

　　When Xiao Ping made her debut in The Wind Rises in the Forest, she was in high spirits. He is Xiao’s son-in-law, and the brightest boy in Jinling. He is young, imposing, supported by his father and brother, and loved by the audience.

　　Because of his free and easy personality since childhood, Xiao Ping Jing’s daily life in Changlin Wangfu was changed from a "group pet" to a "group pet" by her father and eldest brother. Some netizens even proposed to set up a "Caring for Xiao Ping Jing’s Growth Association" for the second son who lives at the bottom of the food chain.

　　In addition to worrying about his bohemian personality, the emotional relationship between Xiao Ping Jing, a family member of "Stupid White Sweet Doctor" and Lin Xi, CEO of Jifengtang, a national pharmaceutical chain, has also attracted much attention. The story of Xiao Ping Jing’s failure to get along with each other can be called "the scene of a big car accident": she called Lin Xi’s maiden name when she didn’t agree with each other, staged a "medical quarrel" when she first met, and regarded the "destiny takes a hand" as a "friend". … The "textbook-level" love-chasing negative textbook makes netizens unable to help but vomit: "Pingjing is single by strength, but it can’t be moved."

　　This cheerful atmosphere did not last long. My father was old, and my eldest brother Xiao Pingzhang died unfortunately. A series of changes forced the young Pingjing to quickly grow into the pillar of Changlin Wangfu.

　　The young swordsman should have walked in the end of the world, but because he was born in Changlin Wangfu, he inherited the character of Changlin Army. Facing the great cause of his home country and the friendship of a thousand years, almost overnight, the young man’s spirited Xiao Ping Jing disappeared, and he gradually changed from an unrestrained "cold pool Little Dragon" to a mature and steady "Huaihua General".

　　When he came back from the north to see his father, Xiao Ping couldn’t afford to kneel in front of his father. He looked up and was in tears. When talking about crying, Haoran Liu admitted that he was not good at it at first. "It may be because of life experience. I have never experienced too sad or too negative, so that kind of emotional crying has always been a hurdle for me." With the maturity of mentality and the deepening of the plot, Haoran Liu’s plays in the later period of Changlin Wangfu are basically in tears. "Crying every day during that time makes it easier to get into a sad mood.".

　　All the crew members are "drama experts" and Kong Sheng is the "hand substitute" of Go.

　　The first time I took a TV series, I expected and appreciated the Noon Sunshine Team, which was an important reason for Haoran Liu’s participation in "A Wind Rises in a Long Forest". The team’s trust in him also made Haoran Liu feel very happy. "I think it is rare that the main role of such a heavy TV series will be played by such a small actor. It is a very happy thing for me as an actor to receive such a role at this age."

　　Regarding the query and speculation on the Internet that he played first hero for the first time in costume drama, Haoran Liu felt that the role of Xiao Ping Jing was very difficult, but if he could finish it, it would be a great help to his performance. "If there is a good script, a character I like, and a director I want to work with, if there is such an opportunity to find me, I should not retreat because of fear or something, so I will do my best."

　　This lush teenager is as free and easy as a teenager. Facts have proved that Haoran Liu’s interpretation was recognized by the audience, and even the teacher Sun Chun, who played Xiao Tingsheng in the play, couldn’t help but praise: "Hao Ran made great progress. In the early stage, Xiao Ping Jing was a little boy, and in the later stage, he came from afar, and I was already in tears."

　　Haoran Liu recalled that the Noon Sunshine Team has always been famous for its rigor and seriousness, and every prop must be true. Even the Jifengtang medicine cabinet, which does not appear in the play, is filled with genuine Chinese herbal medicines, and the prop group teachers can accurately name each medicine.

　　Compared with Jifengtang, there are only a few scenes in the prison. In order to achieve the overall unified effect, the crew did not neglect at all. The creative staff consulted a large number of historical materials, and found a comprehensive reference for the overall design and interior decoration of the prison. The prison was built in strict accordance with the pattern of ancient Yin and Yang, Eight Diagrams and heavenly stems and earthly branches. The team also specially studied many historical documents such as the history of ancient prisons in China, and there are many more examples.

　　What impressed Liu Hao was not only the rigor and seriousness of the behind-the-scenes team, but also the superb acting skills of the team staff. "It is really that everyone in the noon team can perform, and this team is commonly known as ‘ Everyone is a showman ’ All the deputy directors, screenwriters and directors of the martial arts group who are on the scene can play. Sometimes a character with only one or two episodes appears. When I go to the scene, I find that yesterday’s deputy directors have all dressed up. " Kong Sheng, the director who always plays every guide and plays every play, is even more "if he can, he will work harder". He not only acts as a go instructor, but also acts as a substitute in person.

　　Text/reporter Yang Wenjie

Since December 2021 in our city,

Vaccinate HPV vaccine for school-age girls free of charge every year.

the other day

Free vaccination program in 2024

Has been officially launched

In 2024, the implementation scope and vaccination targets of the free vaccination project are:

Born after September 1, 2010 and enrolled in the first half of 2024, a first-year girl from Wuxi;

Other school-age girls who meet the vaccination conditions in Wuxi.

In 2024, HPV vaccination for eligible school-age girls will be organized by the school.

The free vaccine variety is domestic bivalent HPV vaccine, and the recipient does not bear any expenses.

Cervical cancer is the only cancer type that can be prevented by vaccination. 99.7% of cervical cancer is caused by persistent infection of high-risk HPV virus.

The age of HPV infection among ordinary women in China is characterized by "double peaks";

That is, 17-24 years old and 40-44 years old are the two peak ages of HPV infection among Chinese women, and the first peak of infection appears at 17-24 years old, suggesting that HPV vaccine should be vaccinated as soon as possible.

Teenagers are the primary target of HPV vaccine.

The 2017 WHO position paper suggests that:

To prevent cervical cancer, it is suggested that the primary vaccination target of HPV vaccine is girls aged 9-14 who have not had sex;

In 2017, China’s Guidelines for Comprehensive Prevention and Control of Cervical Cancer suggested that:

At present, the recommended age range of HPV vaccination in China is 9-45 years old women, with emphasis on 13-15 years old girls.

Questions and answers on common vaccination of HPV vaccine

one

What are the HPV vaccines currently on the market?

There are more than 200 genotypes of HPV, which can be divided into high-risk and low-risk types according to their potential to induce cancer. At present, 12 types of HPV (16/18/31/33/35/39/45/51/52/56/58/59) are defined as high-risk (carcinogenic) types, among which HPV16 and 18 have the highest carcinogenic risk.

At present, there are three types of HPV vaccines listed in China: bivalent, tetravalent and nonavalent HPV vaccines, of which four are used for women aged 9-45.

See the table below for details.

tips

Different vaccines cover different HPV types, and multivalent HPV vaccines provide more protection for high-risk HPV types, and recipients can choose voluntarily and vaccinate at their own expense.

On January 9th, 2024, two doses of imported nine-valent HPV vaccine for 9-14-year-old women have been approved by National Medical Products Administration, China, and we will adjust the two doses of vaccination procedures for 9-14-year-old women according to relevant documents.

2

How safe is HPV vaccine?

Since the cervical cancer vaccine was launched in the world in 2006, HPV vaccine has been approved for use in more than 130 countries (regions), among which 110 countries (regions) have included HPV vaccine in the national immunization plan, and the cumulative vaccination has exceeded 300 million doses.

HPV vaccine has been used in our city since 2017, and no serious adverse reactions have been reported in the monitoring data, mainly local reactions of redness, swelling and pain, but very few allergic reactions are not excluded.

Most acute allergic reactions occur within 30 minutes after inoculation. To ensure safety, you must stay at the inoculation site for 30 minutes after inoculation, and you can leave only after there is no abnormality.

three

What conditions are not suitable for HPV vaccination?

Those who have hypersensitivity to the active ingredients of the vaccine or any auxiliary ingredients.

Those who have had serious adverse reactions to vaccination.

Pregnant women.

Patients with thrombocytopenia or other coagulation disorders that may become contraindications for intramuscular injection.

Those who are suffering from fever, acute disease, acute attack of chronic disease, or uncontrolled patients with severe chronic diseases should be vaccinated after the disease is cured or stabilized.

four

Can I get HPV vaccine during menstrual period?

If there is no fever, infection, or severe menstrual discomfort, you can get HPV vaccine during menstruation.

five

How long is the protection period of HPV vaccine?

Do you need a booster shot?

At present, a number of research data show that HPV vaccine has a long-term protective effect, and repeated vaccination is not needed to enhance the immune effect.

six

After the second bid, can I bid another four or nine?

At present, there are very few research data about the safety and effectiveness of repeated vaccination of HPV vaccine from different manufacturers, so repeated vaccination is not recommended for the time being. The Advisory Committee on Vaccine Immunization Practice (ACIP) in the United States also clearly stated in the document on HPV vaccination that it is not recommended to vaccinate with nine-valent HPV vaccine after bivalent or tetravalent HPV vaccine.

seven

If you break one of the three stitches in the middle, do you want to start playing again?

The World Health Organization suggests that the HPV vaccine should be given three shots within six months, and the effect is the best.

But if there is a break in the middle, there is no need to restart the vaccination procedure, just finish the rest of the needles!

eight

Halfway through the vaccination procedure,

Can I replace vaccination with different types of HPV vaccine?

Substitution vaccination cannot be interchanged. Even if there are different types of HPV vaccines, you should use the same vaccine from the same manufacturer for each dose.

nine

Can HPV vaccine prevent cervical cancer 100%?

No vaccine can be guaranteed to be 100% effective. Due to physical condition, disease, family history and other factors, the protective effect of vaccine will vary from person to person.

Therefore, after HPV vaccination, it is still recommended that women who have sex after the age of 25 have regular cervical cancer screening.

10

After being infected with HPV, does HPV vaccine still have a protective effect?

Even if you have been infected with a certain type of HPV, you can still get other types of protection by taking HPV vaccine. Epidemiological data show that most HPV infected people in China are infected with a single type, so even if they are infected with HPV, they can still benefit from HPV vaccination.

In addition to the above-mentioned age-appropriate vaccinators,

How should other citizens make an appointment for HPV vaccination?

You need to make an online reservation first.

After the reservation is successful

An appointment for vaccination will be arranged by the vaccination clinic.

Complete the inoculation according to the agreed time.

Original title: "Free vaccination, start again! 》

Read the original text

According to the Shandong Food and Drug Administration, for more than five years, Pangmou and her daughter bought 25 kinds of vaccines for human use, such as influenza and hepatitis B, at low prices from salesmen or vaccine dealers of pharmaceutical companies, and sold them to 24 provinces and cities at a higher price without strict cold chain storage and transportation, valued at 570 million yuan. On the evening of March 19, 2016, Shandong Food and Drug Administration announced that it had sorted out 107 online clues to provide vaccines and biological products to Pang and others, and 193 offline clues to purchase vaccines and biological products from Pang and others, involving 24 provinces and cities across the country.

　 　 Special feature of 1905 film network "When she was young, she was like a flower. Now she is like a tree, which allows many people to enjoy the cool in her shade." This is Hong Kong director Lin Yihua’s evaluation of Zhang Aijia. On March 23rd, director Zhang Aijia’s new film "Missing You" was shown as the opening film of the Hong Kong International Film Festival. With this film, Hong Kong actor Liang Luoshi, who had never met for a long time, also came back to share the warmth and coldness of the bustling city with Joseph Chang, Ke Yulun and Li Xinjie. When we talk about Zhang Aijia again, there are still too many topics worth talking about.

　 　 In his forty-two years as a filmmaker, Zhang Aijia has mastered multiple identities, leaving a deep mark on Hong Kong and Taiwan film circles. As an actress, she won two Golden Horse Awards in Taiwan and two Hong Kong Awards respectively. As a director, from "Little Girl Fishing" to "20 30 40" received rave reviews; As a predecessor, her artists such as Jacklyn Wu, Rene Liu and Li Xinjie are outstanding; As a singer, a song "The Price of Love" has been sung so far; As the owner of an entertainment company, she excavated Yang Dechang and helped Kenneth Bi, known as the "mother of the new wave of Taiwan Province movies"; Even the objects of her scandal are Tayu Lo, Yang Dechang and other industries.

　 　 She studied under Li Hanxiang and Hu Jinquan, cooperated with famous directors from Hong Kong and Taiwan, such as Ang Lee, Xu Anhua, Du Qifeng and Zhang Wanting. She was nominated for the Oscar for Best Supporting Actress for The Red Violin, which was co-produced by Canada and France. She was the first Asian actress to be selected as the focus of the Toronto Film Festival. Now, 23 years later, Zhang Aijia has once again become the "focus shadow" at the Hong Kong International Film Festival which she is familiar with.

Multiple Notes on Feminism: Idealization is Zhang Aijia’s film label.

　 　 When it comes to Zhang Aijia, I have to mention feminism. Her films usually feature women. But everyone has a set of opinions about feminism, and not every annotation is suitable for describing Zhang Aijia’s works. Traditionally, it is believed that the purpose of feminism is to resist and win the rights of men. However, the feminism embodied in Zhang Aijia’s films does not mean to belittle men, but rather reflects the mutual understanding and tolerance between the two sexes, so that men and women can realize their own existence value in an equal relationship. Just like in "Little Girl Fishing", in the face of her boyfriend Jiang Wei’s selfish and disrespectful love, Xiaoyu went from initial resignation to later obedience to inner judgment, and stayed to take care of the sick Mario. This is a woman’s affirmation of self-worth judgment, and it is also a sober reflection after losing herself in love.

　 　 At the end of 1970s and the beginning of 1980s, Hong Kong and Taiwan films, represented by Xu Anhua and Zhang Aijia, rose a feminist trend, which was greatly influenced by contemporary European and American films. Kramer vs. kramer, which won the Oscar in 1979, catered to the new family model of women’s liberation movement, and was widely welcomed by women. In the same year, Tess directed by roman polanski, Deep in My Heart starring sally field in 1984 and many other films triggered worldwide discussions on women’s movies. Zhang Aijia, who has settled in the United States with her mother since childhood, has its natural advantages in feeling the new wave.

　 　 At the same time, there were filmmakers who showed obvious feminist characteristics, as well as Hong Kong directors Xu Anhua and Zhang Wanting. People always liked to compare these three female directors together. However, unlike Xu Anhua’s cold documentary and Zhang Wanting’s euphemistic dream, Zhang Aijia’s handling of female roles was more idealistic. Even if she suffered more hardships, the heroine would eventually get out of the knot and have a cool and positive attitude and a beautiful and stable life. Lily in 20 30 40 experienced her husband’s betrayal and divorce, although she tried to find a different partner. The young and gentle gentleman in Heartbeat, although he has been missing out all his life and can’t get married, both of them live a superior life and turn their regrets into precious memories of life; In Favorite, Wu Mingbao and Bai Yun fell in love with the same man. Finally, Bai Yun left with her child. After decades, the two women met again to recount their past grievances, and there was no more uproar. The ending of Zhang Aijia’s works will never make people feel desperate.

AUO above lover not full captures delicate and ambiguous same-sex feelings.

　 　 Zhang Aijia once mentioned in an interview: "When girls grow up, there must be intimate relationships between women. Such vague feelings are earlier than boys. Later, we will all get married and have children. This feeling will not have any impact on our marriage." The ambiguous feelings between the same sex are also delicate and touching under the lens of Zhang Aijia, such as Chen Li and Xiao Rou in Heart, such as Xiaojie and A Tong in 20 30 40.

　 　 Zhang Aijia’s description of same-sex feelings is more of a hazy and beautiful feeling mixed between friendship and love, but the audience can feel it from the picture. The weight of this kind of memories of youth is enough to be remembered and treasured for a lifetime. In Heartbeat, Chen Li, who has reached middle age, cried and told her husband Haojun to leave, and finally admitted that she had always loved Xiaorou. She and Haojun silently loved the same woman. In "20 30 40", Xiaojie and A Tong bid farewell to the tearful kiss at the airport, which is not only a farewell, but also a beautiful ending for the beautiful friendship gained during the pursuit of "Star Dream".

　 　 Some of this concern for same-sex feelings is very straightforward. For example, in Hainan Chicken Rice directed by Kenneth Bi, Zhang Aijia plays Jane, the mother of three gay sons, who has broken his heart about the sexual orientation of the three sons, but also pays attention to the expression of girlfriends’ feelings. For example, in Yang Dechang’s One Day at the Beach, Zhang Aijia not only has a heart-to-heart relationship with the pianist played by Hu Yinmeng, the ex-girlfriend of his brother, but also has a good girlfriend around him. Same-sex love, appearing in Zhang Aijia’s films, is euphemistic, delicate, fresh and natural between friends and lovers.

　 　 Liang Luoshi, the star of this new work Niannian, once played a homosexual with Rainie Yang in Tattoo, and his handsome tattoo of flowers on the other side is still impressive. This time, I collaborated with Zhang Aijia to "Calm down, slow down" in Missing. Liang Luoshi plays a young female artist, talking with her past, discussing affection and love. Two women who have had a different perspective on same-sex feelings get together to create, which is also considered as a gas field.

　　　　　　 CCTV News:The Central Meteorological Observatory predicts that from tomorrow night, another strong cold air will start from northern Xinjiang and affect most parts of China from west to east. In addition, the 26th typhoon "Seagull" has been generated this year, and most of the Yellow Sea, East China Sea and Taiwan Province Strait will be disturbed by strong winds of 6-8.

　　　　　　 Affected by cold air, the temperature dropped by 4 ~ 10℃ in most parts of central and eastern China yesterday, reaching 12 ~ 18℃ in eastern and southern Northeast China and parts of eastern North China. Snowfall (rain) or sleet in eastern Heilongjiang, eastern Jilin and eastern Liaoning. It is expected that there will be small to medium snow and local heavy snow in central and eastern Jilin and northern Liaoning today, and the temperature in most parts of central and eastern China will rise briefly. From the night of 15th, a new strong cold air will start from the north of Xinjiang and affect most parts of China from west to east. Affected by this, there will be northerly winds of 4 ~ 6 in most parts of China, with the temperature generally dropping by 6 ~ 10℃, and the temperature drop in some areas can reach above 12℃. The wind power in Shankou, Xinjiang can reach 9 ~ 10, and the central and eastern regions are accompanied by a wide range of rain and snow.

　　　　　　 This year’s No.26 typhoon "Seagull" was generated yesterday morning, and it is expected to move to the northwest at a speed of 20-25 kilometers per hour. Due to the joint influence of cold air and typhoon "Seagull", most of the Yellow Sea, most of the East China Sea, Taiwan Province Strait, east of Taiwan Province, bashi channel, most of the South China Sea, Beibu Gulf and Qiongzhou Strait will have a gust of 6-8 from the day of 14th to the night of 16th.

　　In 2024, the Mercedes -EQE pure electric SUV was redesigned. Under the condition that the guide price of the new car remained unchanged, the 215kW 350 model was cancelled, and all the models were 500 models with a total power of 300kW, which was high at the beginning. EQE 500 4MATIC Ultimate, the top model, adds AIRMATIC air suspension system, which can automatically lift the body up to 25mm according to the road conditions. Standard 10 rear wheel steering makes the turning radius only 10.5 meters. In addition, the whole system has added velvet foot pads, 5G communication technology (free unlimited traffic for 3 years) and UWB digital keys, and carrying authorized digital devices (smart phones/smart watches) can unlock the starting vehicles.

　　The 2024 modified Mercedes-Benz EQE pure electric SUV has the same appearance and interior as the 2023 model, so this time I mainly talk about its endurance performance and driving experience. This test drive is EQE pure electric SUV 500 4MATIC deluxe edition, and the route is from Tianjin downtown to Yizhuang, Beijing. 90% of the whole journey is an expressway with a speed limit of 110km/h, which is also the most challenging road condition for pure electric vehicles.

　　Mercedes-Benz EQE pure electric SUV is equipped with a 96.1kWh ternary lithium battery, which has a full battery life of 609km(CLTC). Before departure, the battery capacity is 97%, and the maximum cruising range is 606km. The whole process adopts "C" comfort mode, the kinetic energy recovery is D (intelligent kinetic energy recovery), and the air conditioner is set at 22℃, carrying two people and a small amount of luggage. High-speed basically runs against the speed limit, and often accelerates to overtake the local train. The minimum power consumption is 15.9kWh/100km. After the final driving of 111km, the apparent power consumption is 18.0kWh/100km, which is similar to the official claim of 17kWh/100km by Mercedes-Benz.

　　The whole journey shared 22% of the electricity and ran 111km. It is estimated that under this road condition, the full battery life can reach about 505km. For a 2.6-ton medium and large pure electric SUV, this power consumption performance is very satisfactory, which is similar to that of many other brands of medium and large cars. In addition, it will also give two remaining cruising ranges (454km and 471km). The less one is the cruising range if you drive harder, and the more one is the cruising range if you drive more smoothly. It will always learn your driving style and calculate the remaining cruising range in real time in combination with road conditions.

　　Why is it so energy-saving? Mercedes-Benz EQE pure electric SUV is developed based on EVA pure electric platform, and its electric drive efficiency is as high as 94%, making full use of every kilowatt hour. In addition, the front motor can be disconnected from the half shaft within 240 milliseconds, which makes the sliding distance longer and prolongs the total cruising range. The most important thing is that the drag coefficient of the whole vehicle is only 0.25Cd, which improves the cruising range by means of low drag design such as bow-shaped body, low drag wheel hub, closed middle net and smoother and narrower sheet metal gap.

　　Mercedes-Benz EQE pure electric SUV has four kinetic energy recovery modes, namely D- (strong recovery), D (standard recovery), D+ (no recovery) and D auto (intelligent recovery). The most interesting thing is the intelligent kinetic energy recovery mode, which can judge the road ahead with environment-aware hardware and automatically adjust the kinetic energy recovery intensity. For example, when the accelerator pedal is released on the road ahead, it will automatically adopt the D+ sliding mode, and because the electric vehicle has no engine braking effect, the speed drops slowly and the sliding distance is very far. When the road ahead is congested, it will automatically adopt D- or D kinetic energy recovery to slow down the speed in time. If you don’t know which kinetic energy recovery mode to choose, choosing D auto is the simplest method, and its judgment is also very reliable, which not only ensures comfort, but also gives the battery some electricity.

　　In intelligent driving assistance, Mercedes-Benz EQE pure electric SUV has L2 driving assistance, ACC adaptive cruise+lane keeping, which can greatly alleviate the fatigue of long-distance high-speed driving. At the same time, it also has the function of shifting the steering rod to change lanes. After shifting the steering rod, the vehicle can automatically change lanes and accelerate to the speed of constant speed cruise on the premise that the system judges the rear safety, which is still very convenient.

　　Let’s talk about the driving experience again. The front and rear dual motors of Mercedes-Benz EQE pure electric SUV output a total of 300 kW/858 N m, except in E economy mode, which will limit the motor power. In C comfort mode and S sports mode, it behaves like a beast. A big guy who accelerates for 5.1 seconds in 100 kilometers can also make people’s blood boil when they get angry. And the power is from 10% to 100%, and it can be fully output.

　　It is worth mentioning that such a large SUV does not look up and nod too obviously, whether it is in sudden acceleration or sudden braking. There are probably two reasons for this. One is that thanks to the EVA pure electric platform, the four wheels are closer to the four corners of the car body, which physically inhibits the range of raising the head and nodding; Second, Mercedes-Benz has rich experience and foundation in suspension design and excellent support. A lot of new energy vehicles have been tested before, and the SUV that accelerates for about 5 seconds has a relatively large head-up and nodding range, which will inevitably cause discomfort to passengers in the car.

　　The suspension adjustment of Mercedes-Benz EQE pure electric SUV is relatively moderate, and it retains strong support in comfort. It is comfortable enough for home use, and you can occasionally run wild when driving by yourself. The direction is accurate, and the sense of the road is also preserved. The road information is not completely isolated, and the driver can communicate better with the vehicle. In NVH performance, there is basically no wind noise when driving at high speed, only slight tire noise but it is not disturbing. In addition, we simply tried to ride the flagship model with air springs, which made the road vibration filter more thorough and more comfortable.

　　The design of Mercedes-Benz EQE pure electric SUV is still the elegant beauty that is not too ostentatious. Inherited the unique design language of EQ family, the closed front grille and the three-pronged star emblem mesh complement each other, and the dynamic EQ design language shows the beauty of freedom and easy, with optional "meteor shower" intelligent digital headlights, providing up to 2.6 million lighting pixels.

　　The side of the vehicle adopts the "arch" body design, which brings smoother and more dynamic lines while reducing wind resistance. Its wheelbase has reached 3030mm, and its body size is 4880/2032/1679mm.

　　The tail of Mercedes-Benz EQE pure electric SUV is round and full, and the taillight adopts a penetrating 3D spiral taillight with four spirals inside. It is worth mentioning that if you see five spirals, it is its big brother-Mercedes-Benz EQS pure electric SUV.

　　The interior of Mercedes-Benz EQE pure electric SUV looks more like sitting in a yacht, elegant and dignified. The standard 12.8-inch central control panel integrates the latest MBUX intelligent human-computer interaction system, and adopts 8-core CPU, 24GB storage and 46.4GB memory bandwidth per second. The top model is a super-linked screen composed of three screens.

　　MBUX adopts zero-level menu, and common functions such as air conditioning, music and navigation are all put on the interface. In addition, the physical buttons such as driving mode, vehicle setting and volume adjustment are reserved, which is more convenient to use.

　　Off-road mode and transparent chassis are still very useful for an SUV. When encountering road conditions with poor vision, they will help you grasp the environment and vehicle status of the vehicle in time.

　　Finally, I have to mention the HUD of Mercedes-Benz, which is not only large enough, but also clear enough. The most important thing is that the information displayed is quite rich. In addition, the visual distance projected by it is far enough, and the eyes will not feel tired after long-term use. If you don’t like HUD, you can turn it off by voice control. Mercedes-Benz’s "mind-reading voice assistant" can support natural semantic control, and there are many controllable vehicle settings, and the localization design is in place. In addition, Mercedes-Benz will start the largest OTA upgrade this year, and the "mind-reading voice assistant" will have stronger understanding and execution of continuous instructions, and the response speed of the second-generation MBUX intelligent human-computer interaction system will increase by 31%.

　　I won’t go into details about the seat space here, please click the link below to view it:

　　> > > > > The road to luxury with electricity is to test drive the Mercedes EQE SUV.

　　In this activity, we also visited the Mercedes-Benz China R&D Technology Center in Beijing to see how strict Mercedes-Benz EQE pure electric SUV and Mercedes-Benz’s standards for building cars are.

　　Mercedes-Benz EQE pure electric SUV is not only equipped with noise reduction hardware such as VSG acoustic glass and vehicle acoustic package, but also pays more attention to noise balance adjustment. In Mercedes-Benz, the noise balance of the whole vehicle is more important than simply reducing the decibel value. In addition, the annoying low-frequency noise is mainly produced by the structure of the car body and chassis, which is difficult to improve later. Mercedes-Benz has carried out full simulation verification in the early stage of vehicle development to iterate the design of body and chassis, and effectively suppress the low-frequency noise of the whole vehicle. In addition, for SUV models, a major source of low-frequency noise is the tailgate. Only by adopting higher body rigidity can low-frequency noise be avoided. The torsional rigidity of Mercedes-Benz EQE pure electric SUV is 45,800 nm/.

　　Mercedes-Benz is the first automobile brand in China to introduce sunshine simulator, which restores the real use environment of customers at any cost and creates a cockpit travel experience that meets Mercedes-Benz comfort and energy efficiency standards. The sunlight simulator can simulate the high temperature of 50℃ in Turpan, the sunshine of 16 hours a day like Altay, and the relative humidity of 95%, so that the temperature inside the car can reach 70℃ at the highest. Through the high-strength test of sunlight simulator, the air conditioning comfort, air conditioning energy efficiency and heat insulation performance of sunroof and windshield of EQE pure electric SUV can be accurately evaluated.

　　It is here that the official cruising range of Mercedes-Benz electric vehicles is measured. It is worth mentioning that Mercedes-Benz also has strict standards for the electromagnetic radiation of electric vehicles that are highly concerned by users. Every component of Sandian has to pass the EMC test of the same standard, and the test standard of Mercedes-Benz is higher than the national standard.

　　Based on the accumulation of more than 130 years, Mercedes-Benz summed up the "Mercedes-Benz Driving Character", which is a set of chassis systematic standards, covering five dimensions of driving comfort, safety, driving confidence, sportiness and accuracy, and can quantify human subjective perception into more than 130 objective KPI data, and measure it through 40 sensors covering more than 100 directions. Mercedes-Benz suspension will not blindly seek softness, simple softness will lose the sense of road, which will make passengers’ senses mismatch, which will easily lead to motion sickness; For different road incentives, the secret of driving comfort is to be soft when soft and hard when hard. This is why the suspension adjustment of Mercedes-Benz EQE pure electric SUV is relatively moderate from the actual driving experience, and it retains certain support while being comfortable.

　　In April 2021, EQS, the first model based on Mercedes-Benz EVA pure electric platform, was officially released. In more than three years, based on this platform, Mercedes-Benz has launched a number of pure electric vehicles such as EQE, EQE pure electric SUV and EQS pure electric SUV. More than that, with the arrival of MMA pure electric platform, Mercedes-Benz pure electric vehicles will also be more competitive. At the 2024 annual meeting of China Development Forum held on March 24 this year, Ola K?llenius, Chairman of the Board of Directors of Mercedes-Benz Group Co., Ltd. said: Mercedes-Benz will firmly transform into an electric vehicle. Mercedes-Benz Modular Architecture (MMA) platform will be launched, marking the next step towards the electric future. Beijing Benz will launch vehicles based on MMA platform, including the long wheelbase version for China market. In addition, platforms such as MB.EA, AMG.EA and VAN.EA will be launched later, and each model of Mercedes-Benz in the future will bring corresponding pure electric product choices to customers.

　　Electric switch, pure electricity is still running.